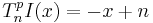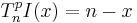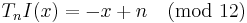Inversion (music)
In music theory, the word inversion has several meanings. There are inverted chords, inverted melodies, inverted intervals, and (in counterpoint) inverted voices. The concept of inversion also plays a role in musical set theory.
Contents |
Inverted intervals
An interval is inverted by raising or lowering either of the notes using displacement of the octave (or octaves) so that both retain their names (pitch class). For example, the inversion of an interval consisting of a C with an E above it is an E with a C above it - to work this out, the C may be moved up, the E may be lowered, or both may be moved.
Under inversion, perfect intervals remain perfect, major intervals become minor and the reverse, augmented intervals become diminished and the reverse. (Double diminished intervals become double augmented intervals, and the reverse.) Traditional interval names add together to make nine: seconds become sevenths and the reverse, thirds become sixes and the reverse, and fourths become fifths and the reverse. Thus a perfect fourth becomes a perfect fifth, an augmented fourth becomes a diminished fifth, and a simple interval (that is, one that is narrower than an octave) and its inversion, when added together, will equal an octave. See also complement (music).
| Interval quality under inversion | |
|---|---|
| Perfect | Perfect |
| Major | Minor |
| Augmented | Diminished |
| Interval name under inversion | |
|---|---|
| Unison | Octave |
| Second | Seventh |
| Third | Sixth |
| Fourth | Fifth |
Inverted chords
A chord's inversion describes the relationship of its bass to the other tones in the chord. For instance, a C major triad contains the tones C, E and G; its inversion is determined by which of these tones is used as the bottom note in the chord.
The term inversion is often used to categorically refer to the different possibilities, although it may also be restricted to only those chords where the bass note is not also the root of the chord (see root position below). In texts that make this restriction, the term position may be used instead to refer to all of the possibilities as a category.
Root position
A root-position chord is sometimes known as the parent chord of its inversions. For example, C is the root of a C major triad and is in the bass when the triad is in root position; the 3rd and the 5th of the triad are sounded above the bass. Thus, a root-position chord is also known as a 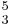 chord.
chord.
The following chord is also a C major triad in root position, since the root is still in the bass. The rearrangement of the notes above the bass into different octaves (here, the note E) and the doubling of notes (here, G), is known as voicing.
Inversions
In an inverted chord, the root is not in the bass (i.e., is not the lowest note). The inversions are numbered in the order their bass tones would appear in a closed root position chord (from bottom to top).
In the first inversion of a C major triad , the bass is E—the 3rd of the triad—with the 5th and the root stacked above it (the root now shifted an octave higher), forming the intervals of a 3rd and a 6th above the inverted bass of E, respectively. A first-inversion triad is also known as a 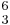 chord.
chord.
In the second inversion , the bass is G—the 5th of the triad—with the root and the 3rd above it (both again shifted an octave higher), forming a 4th and a 6th above the (inverted) bass of G, respectively. A second-inversion triad is also known as a 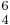 chord. This inversion can be either consonant or dissonant , and analytical notation sometimes treats it differently depending on the harmonic and voice-leading context in which it occurs (e.g. see Cadential six-four chord below).
chord. This inversion can be either consonant or dissonant , and analytical notation sometimes treats it differently depending on the harmonic and voice-leading context in which it occurs (e.g. see Cadential six-four chord below).
Third inversions exist only for chords of four or more tones, such as 7th chords. In a third-inversion chord , the 7th of the chord is in the bass position. For example, a C major 7th chord in third inversion consists of B in the bass position, with C, E and G above it— being intervals of a 2nd, 4th and 6th above the (inverted) bass of B, respectively. (, , )
Notating root position and inversions
Figured bass
Figured bass is notation convention used to specify chord inversion, in which Arabic numerals (figures) are written (placed vertically, in descending numerical order) below the bass note of each chord in a harmonic progression, expressing the intervals resulting from the voices above it (usually assuming octave equivalence).
For example, in root-position triad C-E-G, the intervals above bass note C are a 3rd and a 5th, giving the figures 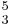 . If this triad were inverted (e.g. E-G-C), the figures (
. If this triad were inverted (e.g. E-G-C), the figures ( 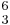 ) would apply, due to the intervals of third and sixth appearing above bass note E. Figured bass is similarly applied to 7th chords, which have four tones.
) would apply, due to the intervals of third and sixth appearing above bass note E. Figured bass is similarly applied to 7th chords, which have four tones.
Certain arbitrary conventions of abbreviation (and sometimes non-abbreviation) exist in the use of figured bass. In chords whose bass notes appear without symbols, 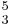 position is to be understood by default. First-inversion triads (
position is to be understood by default. First-inversion triads ( 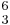 ) are customarily abbreviated as
) are customarily abbreviated as 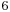 , i.e. presence of the 3rd is understood. Second-inversion triads (
, i.e. presence of the 3rd is understood. Second-inversion triads ( 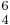 ) are not abbreviated. Root-position seventh-chords, i.e. 7-5-3, are abbreviated as
) are not abbreviated. Root-position seventh-chords, i.e. 7-5-3, are abbreviated as 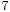 . First inversion seventh-chords 6-5-3, are abbreviated as
. First inversion seventh-chords 6-5-3, are abbreviated as 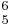 . Second inversion seventh-chords 6-4-3, are abbreviated as
. Second inversion seventh-chords 6-4-3, are abbreviated as 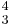 . Third inversion seventh-chords 6-4-2 are abbreviated as
. Third inversion seventh-chords 6-4-2 are abbreviated as 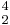 .
.
Figured bass numerals express distinct intervals in a chord only as they relate to the bass voice. They make no reference to the key of the progression (unlike roman-numeral harmonic analysis); They do not express intervals between pairs of upper voices themselves (for example, in a C-E-G triad, figured bass is unconcerned with the interval relationship E-G); They do not express tones in upper voices which double, or are unison with, the bass note. However, the figures are often used on their own (without the bass) in music theory simply to specify a chord's inversion. This is the basis for the terms given above such as "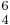 chord"; similarly, in harmonic analysis the term
chord"; similarly, in harmonic analysis the term 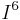 refers to a tonic triad in first inversion.
refers to a tonic triad in first inversion.
Popular-music notation
A notation for chord inversion often used in popular music is to write the name of a chord followed by a forward slash and then the name of the bass note. For example, the C chord above, in first inversion (i.e., with E in the bass) may be notated as C/E. This notation works even when a note not present in a triad is the bass; for example, F/G is a way of notating a particular approach to voicing a F11th chord (G–F–A–C). (This is quite different from analytical notations of function; e.g., the use of IV/V or S/D to represent the subdominant of the dominant).
Lower-case letters
Lower-case letters may be placed after a chord symbol to indicate root position or inversion.[4] Hence, in the key of C major, the C major chord below in first inversion may be notated as Ib, indicating chord I, first inversion. (Less commonly, the root of the chord is named, followed by a lower-case letter: Cb). If no letter is added, the chord is assumed to be in root inversion, as though a had been inserted.
Hindu-Arabic numerals
A less common notation is to place the number 1, 2 or 3 etc. after a chord to indicate that it is in first, second, or third inversion respectively. The C chord above in root position is notated as C, and in first inversion as C1. (This notation is quite different from the Hindu-Arabic numerals placed after note names to indicate the octave of a tone, typically used in acoustical contexts; for example, C4 is often used to mean the single tone middle C, and C3 the tone an octave below it.)
Cadential six-four chord (or Appoggiatura six-four chord)
The cadential 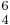 (Figure 3) is a common harmonic device that can be analyzed in two contrasting ways: the first labels it as a second-inversion chord; the second treats it instead as part of a horizontal progression involving voice leading above a stationary bass.
(Figure 3) is a common harmonic device that can be analyzed in two contrasting ways: the first labels it as a second-inversion chord; the second treats it instead as part of a horizontal progression involving voice leading above a stationary bass.
- In the first designation, the cadential
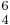 chord features the progression:
chord features the progression: 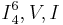 . Most older harmony textbooks use this label, and it can be traced back to the early 19th century.[6]
. Most older harmony textbooks use this label, and it can be traced back to the early 19th century.[6] - In the second designation, this chord is not considered an inversion of a tonic triad[7] but as a dissonance resolving to a consonant dominant harmony.[8] This is notated as
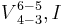 , in which the
, in which the 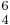 is not the inversion of the
is not the inversion of the 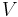 chord, but a dissonance that resolves to
chord, but a dissonance that resolves to 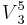 (that is,
(that is, 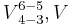 ). This function is very similar to the resolution of a 4–3 suspension. Several modern textbooks prefer this conception of the cadential
). This function is very similar to the resolution of a 4–3 suspension. Several modern textbooks prefer this conception of the cadential 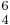 , which can also be traced back to the early 19th century.[9]
, which can also be traced back to the early 19th century.[9]
Counterpoint
Contrapuntal inversion requires that two melodies, having accompanied each other once, do it again with the melody that had been in the high voice now in the low, and vice versa. Also called "double counterpoint" (if two voices are involved) or "triple counterpoint" (if three), themes that can be developed in this way are said to involve themselves in "invertible counterpoint." The action of changing the voices is called "textural inversion".
Invertible counterpoint can occur at various intervals, usually the octave (8va), less often at the 10th or 12th. To calculate the interval of inversion, add the intervals by which each voice has moved and subtract one. For example: If motive A in the high voice moves down a 6th, and motive B in the low voice moves up a 5th, in such a way as to result in A and B having exchanged registers, then the two are in double counterpoint at the 10th ((6+5)–1 = 10).
Invertible counterpoint achieves its highest expression in the four canons of J.S. Bach's Art of Fugue , with the first canon at the octave, the second canon at the 10th, the third canon at the 12th, and the fourth canon in augmentation and contrary motion. Other exemplars can be found in the fugues in G minor and B-flat major [external Shockwave movies] from Book II of Bach's Well-Tempered Clavier, both of which contain invertible counterpoint at the octave, 10th, and 12th.
Inverted melodies
When applied to melodies, the inversion of a given melody is the melody turned upside-down. For instance, if the original melody has a rising major third, the inverted melody has a falling major third (or perhaps more likely, in tonal music, a falling minor third, or even some other falling interval). See m. 24 of Bach's C#m fugue [external Shockwave movie], Well-Tempered Clavier 2, for an example of the subject in its melodic inversion.
Similarly, in twelve-tone technique, the inversion of the tone row is the so-called prime series turned upside-down, and is designated TnI.
Given a certain prime set, with general element pi,j; under the inversion operation, pi,j→I(pi, 12 - j); that is, each element of the prime set is mapped into an element with identical order number but with set number the complement (mod.12) [sic] of the original set number.—Babbitt 1992, 16[10]
each element p of [a given set] P is associated with one and only one inverse element s equals p' in [the universal set] S.—Forte 1964, 144[11]
For each u and v in S (v may possibly equal u), we shall define an operation Iv/u, which we shall call 'u/v inversion.'...
...[W]e conceive any sample s and its inversion I(s) [...] as balanced about the given u and v in a certain intervallic proportion. I(s) bears to v an intervallic relationship which is the inverse of the relation that s bears to u.—Lewin 1987, 50[12]
Inversional equivalency
Inversional equivalency or inversional symmetry is the concept that intervals, chords, and other sets of pitches are the same when inverted. It is similar to enharmonic equivalency and octave equivalency and even transpositional equivalency. Inversional equivalency is used little in tonal theory, though it is assumed a set which may be inverted onto another are remotely in common. However, taking them to be identical or near-identical is only assumed in musical set theory.
All sets of pitches with inversional symmetry have a center or axis of inversion. For example, the set C–E–F–F♯–G–B has one center at the dyad F and F♯ and another at the tritone, B/C, if listed F♯–G–B–C–E–F. For C–E♭–E–F♯–G–B♭ the center is F and B if listed F♯–G–B♭–C–E♭–E.[13]
Musical set theory
In musical set theory inversion may be usefully thought of as the compound operation transpositional inversion, which is the same sense of inversion as in the Inverted melodies section above, with transposition carried out after inversion. Pitch inversion by an ordered pitch interval may be defined as:
which equals
First invert the pitch or pitches, x = −x, then transpose, −x + n.
Pitch class inversion by a pitch class interval may be defined as:
Inversion about a pitch axis is a compound operation much like set theory's transpositional inversion, however in pitch axis inversion the transposition may be chromatic or diatonic transposition.
Pitch axis
In jazz theory, a pitch axis is the center about which a melody is inverted.[14]
The "pitch axis" works in the context of the compound operation transpositional inversion, where transposition is carried out after inversion, however unlike musical set theory the transposition may be chromatic or diatonic transposition. Thus if D-A-G (P5 up, M2 down) is inverted to D-G-A (P5 down, M2 up) the "pitch axis" was or will be D. However, if it is inverted to C-F-G the pitch axis is G while if the pitch axis is A, the melody will invert to E-A-B.
Note that the notation of octave position may determine how many lines and spaces appears to share the axis. The pitch axis of D-A-G and its inversion A-D-E will either appear to be between C/B♮ or the single pitch F.
History
In the theories of Rameau (1722), chords in different positions were considered functionally equivalent. However, theories of counterpoint before Rameau spoke of different intervals in different ways, such as the regola delle terze e seste ("rule of sixths and thirds") which required the resolution of imperfect consonances to perfect ones, and would not propose a similarity between 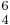 and
and 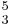 sonorities, for instance.
sonorities, for instance.
See also
References
- ^ Schuijer (2008), p.66.
- ^ Adapted from Measures 14–16, Parry H (1897) "Rustington". In: The Australian hymn book: harmony edition, 1977, p. 492.
- ^ The root-position triad at the end has no 5th above the root. This is common at cadences as a consequence of the voice leading.).
- ^ Lovelock, William (1981), The Rudiments of Music, London: Bell & Hyman, p. ?, ISBN 0713507446.
- ^ Adapted from Piston W (1962) Harmony, 3rd ed., NY, Norton, p. 96.
- ^ Weber, Theory of musical composition, p. 350, quoted in Beach, D (1967) "The functions of the six-four chord in tonal music", Journal of Music Theory, 11(1), p. 8
- ^ Aldwell, Edward; Schachter, Carl (1989), Harmony and Voice Leading (2 ed.), San Diego, Toronto: Harcourt Brace Jovanovich, p. 263, ISBN 0155315196, OCLC 19029983, "The chord does not act as an inversion of I 5/3; it serves neither to extend it nor to substitute for it." LCC MT50 A444 1989.
- ^ Forte, Allen (1974), Tonal Harmony in Concept and Practice (2 ed.), NY: Holt, Rinehart and Winston, p. 68, ISBN 0030774950.
- ^ Arnold, F.T. The art of accompaniment from a thorough-bass, Vol. 1, p. 314. ISBN 0486431886. quoted in Beach, David (1967). "The functions of the six-four chord in tonal music", p.7, Journal of Music Theory, 11(1).
- ^ Schuijer, Michiel (2008). Analyzing Atonal Music, p.67. ISBN 978-1-58046-270-9.
- ^ Schuijer (2008), p.69.
- ^ Schuijer (2008), p.72.
- ^ Wilson, Paul (1992), The Music of Béla Bartók, pp. 10–11, ISBN 0-300-05111-5.
- ^ Pease, Ted (2003). Jazz Composition: Theory and Practice, p.152. ISBN 0876390017.
|
|||||